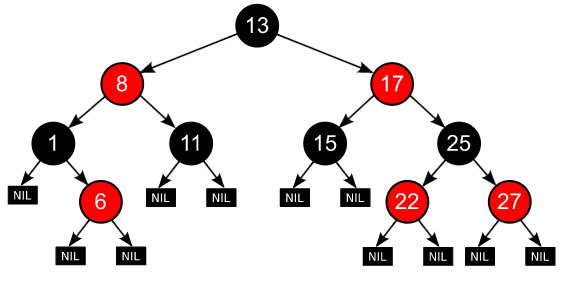
红黑树
简介
红黑树是一种自平衡二叉查找树。它具有下面5大性质:
- 每个节点要么是黑色,要么是红色。
- 根节点是黑色。
- 叶子节点(NIL)为黑色的空节点。
- 红色节点的儿子一定为黑色。
- 任意一个节点到其每个叶子节点的简单路径包含相同数量的黑色节点。
根据以上性质可以看出:任意一个节点出发到其叶子节点,没有一条路径会大于其他路径的两倍。维持了相对的平衡状态。
基本操作
红黑树维护平衡主要靠右旋,左旋,变色。如果不理解右旋与左旋可以看AVL树的介绍。
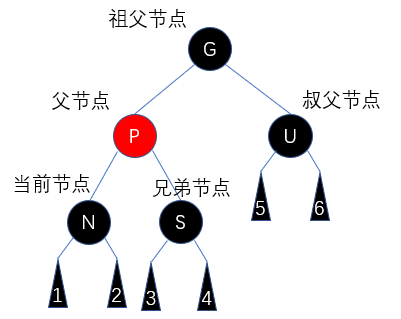
先来约定一下各节点的叫法:
插入
先将红黑树视为二叉查找树,按照其方法插入。
为了不会让某条路径多出1个黑色节点,我们默认插入节点为红色。
根据插入节点位置不同,插入后可能会分为下面几种情形,需要通过不同方法将其旋转,着色,使之成为红黑树。
Case 1
如果当前节点为根节点。为了满足性质二,需要将节点置为黑色。
Case 2
如果父节点为黑色。那么没有性质受到破坏,可以直接插入。
Case 3
如果父节点为红色,叔父节点为红色。
- 将父节点与叔父节点染成黑色。祖父节点染成红色。
- 将祖父节点当成插入节点进行各种情况的检查。
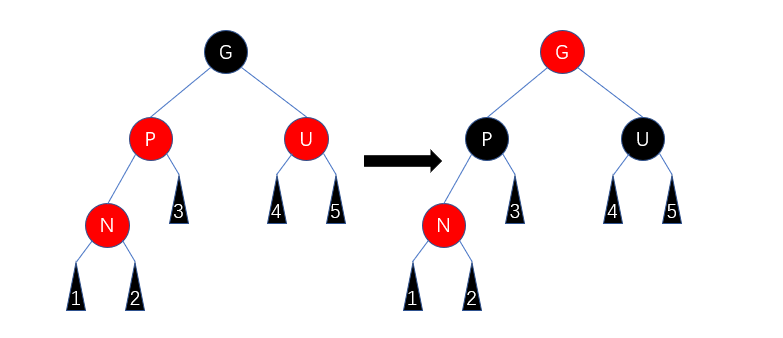
Case 4
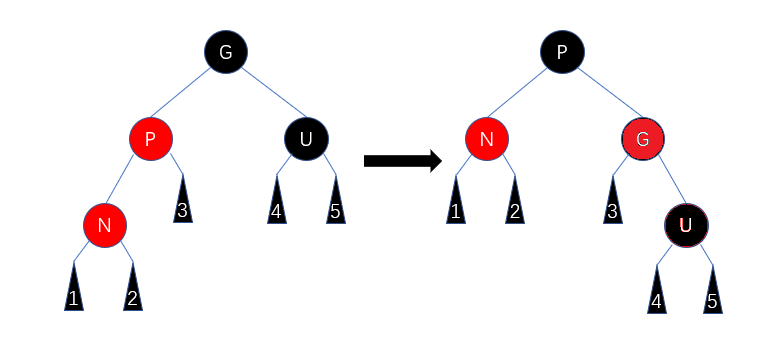
如果父节点为红色,叔父节点为黑色。
- 如果当前节点为父节点的右儿子,父节点为祖父节点的左儿子,对父节点进行左旋。
- 如果当前节点为父节点的左儿子,父节点为祖父节点的右儿子,对父节点进行右旋。
- 将原父节点当成插入节点跳转Case 5。
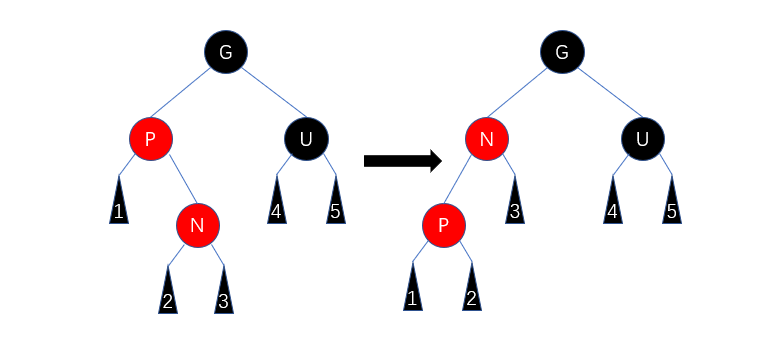
Case 5
如果父节点为红色,叔父节点为黑色。
- 如果当前节点为父节点的左儿子,父节点为祖父节点的左儿子。切换父节点与祖父节点的颜色,并对祖父节点进行右旋转。
- 如果当前节点为父节点的右儿子,父节点为祖父节点的右儿子,切换父节点与祖父节点的颜色,并对祖父节点进行左旋转。
删除
在红黑树中,对于某个节点的删除操作,如果这个节点有两个儿子(非NIL)。我们可以找到其左子树的最大元素或右子树的最小元素将其替换(只替换值,不替换颜色),再将找到的节点删除。
而且因为找到的节点一定不会存在两个儿子,所以接下来我们只需要讨论不超过1个儿子的节点的删除即可。
如果删除节点为红色。那么可以直接用其儿子去代替它。
如果删除节点为黑色,儿子节点为红色。需要先将其儿子染成黑色,再用其儿子代替他。
接下来讨论的都是删除节点与其儿子均为黑色的情况下,预先做平衡处理。
处理是为了让通过删除节点的路径多出一个黑色节点长度,处理完成后再将节点删去,保持性质5的成立。
Case 2、5、6假定删除节点为父节点的左儿子,否则这些情况的左和右将对调。
Case 1
如果父亲节点为根,且删除节点没有儿子。不需要做平衡处理。
Case 2
兄弟节点为红色,父节点为黑色。
对调父节点与兄弟节点的颜色,对父节点进行左旋转,跳转Case4、5、6。
Case 3
兄弟节点和兄弟节点的儿子节点均为黑色,父节点为黑色。
将兄弟节点变为红色,重新对父节点做平衡处理。
Case 4
兄弟节点和兄弟节点的儿子节点均为黑色,父节点为红色。
对调父节点与兄弟节点的颜色。
Case 5
兄弟节点为黑色,兄弟节点的右儿子为黑色,兄弟节点的左儿子为红色。
- 对调兄弟节点与兄弟节点的左儿子的颜色。
- 对兄弟节点进行右旋转。
- 跳转Case 6。
Case 6
兄弟节点为黑色,兄弟节点的右儿子为红色。
- 交换父亲节点与兄弟节点的颜色。
- 将兄弟节点的右儿子染成黑色。
- 对父节点进行左旋转。
查找
红黑树的查找同二叉查找树一样,这里就不过多介绍。
优点
红黑树在查询,插入,删除上的复杂度均为 O(log_n),红黑树与AVL树类似,都平衡了二叉查找树的高度,避免退化成链的风险。
与其不同的是红黑树操作过程中不需要递归,意味着他的旋转次数远不比AVL树多。它牺牲了平衡性以换取少量的旋转操作。在对于存在大量修改的场景性能整体高于AVL树。
- 感谢你赐予我前进的力量



